Conway's Life (Game Of Life, GOL) is the most well known cellular automaton. It has been extensively explored, and a large number of extraordinary patterns have been found. Perhaps to call it a game is somewhat misleading. It's not a game like Doom or other games you would play with a joystick. Life is more of a simulation where you can alter the parameters but you cannot actually alter the outcome directly; that is done by the conditions of the simulation.
The game is played on a 2-dimensional grid. Each cell can be either "on" or "off". Each cell has eight neighbors, adjacent across the sides and corners of the square. The Life rule can be simply expressed (in terms of the way it affects a cell's behavior from one generation to the next) as follows:
A commonly used shorthand for this is 23/3 (or S23/B3), which signifies that a living cell survives if it has two live neighbors, and is born if it has three alive neighbors.
These specific rules were selected in 1970 by the mathematician J.H. Conway to guarantee that the cellular automaton is on the boundary between unbounded growth and decay into dullness. It was proven that its chaotic behavior is unpredictable and it could be used to build a universal Turing-machine and even a universal constructor. The contrast between the simplicity of this rule and the complexity of the behavior it produces is a constant source of wonder.
Note that each cell acts independently based on the old arrangement to produce a new one. The number of neighbors is counted from the old arrangement only. Therefore, if a dead cell has 3 neighbors, the cell will be alive in the next generation, even if those neighbors die.
You can read much more about the history of Cellular Automata here.
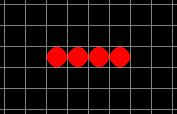
Let’s calculate some generations by hand. Consider the following starting pattern, where empty fields represent 'off' (dead) cells and red dots represent 'on' (living) cells:

In order to be able to apply Conway’s rules (Survival 2,3 / Birth 3) to the pattern we must calculate the counts of alive neighbors for each cell:
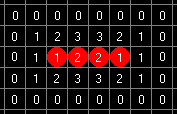
What will happen to living cells? Alive cells can survive when they have either 2 or 3 neighbors. Two central dots have exactly 2 living neighbors, so they will survive. Two other dots have only 1 neighbor; they will die of loneliness.
What will happen to empty cells? Four of them have exactly 3 neighbors; those four cells will become alive. The rest of empty cells will stay off - they have only 0, 1 or 2 neighbors.
So the next generation is as follows:
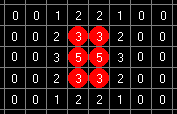
4 cells will survive (the ones with 3 neighbors). Two other cells have to die of crowd.
2 empty cells have 3 neighbors and will come alive. The rest will stay off.
So the third generation is:

And now? No cells have 3 neighbors, so no new cells will come alive. All alive cells have exactly 2 neighbors, so all of them will survive. We have reached a stable pattern (still life) that will not change in next generations.
You can read more about alternative Life rules in Other rules in Life.
John Horton Conway, a British mathematician at Gonville and Caius College, University of Cambridge, was playing around in the late 1960's with a few ideas for a simple cellular automaton. The first ideas for cellular automata were thought of by Ulam. John von Neumann used this idea to create complex cellular automata, which was able to produce non-trivial self-reproducing patterns. John von Neumann's machine has 29 states, however, so Conway was looking for something simple, yet interesting. More specifically, he defined the following criteria:
There should be no initial pattern for which there is a simple proof that the
population can grow without limit.
There should be initial patterns that apparently do grow without limit.
There should be simple initial patterns that grow and change for a considerable period of
time before coming to an end in three possible ways:
Conway and his graduate students played around with various rules, finally settling on the familiar "birth on 3 / survival on 2 or 3" rule. In those days (pre-1970), computers were very primitive, so most of the team's explorations were done with physical checker pieces. One of their greatest discoveries was the glider, which they found while trying to determine whether the R-pentomino was an infinite growth pattern.
The game was first published in the Scientific American in October 1970, in Martin Gardner's "Mathematical Games" column. A few other columns and articles appeared later, but there were more results than Scientific American could reasonably be expected to publish, so the LifeLine quarterly newsletter was invented, and it ran for 11 consecutive issues.
Not much more happened in the Life universe between 1974 and 1988. Then the appearance of more powerful computers, the availability of e-mail over the Internet, and ideas about search engines created something of a Cambrian explosion in the Life universe, which continues to this day.
Life is not limited to "23/3" rules. Other variations on the specific neighbor counts in the rules have been tried, but Conway's formulation seems to have generated more interest than all of the rest combined. Maybe that's partly due to self-generating popularity, and if Conway had specified other rules, probably those would be it.
Most alternative rules are not as simple, or let the universe die out too quickly, or create an exploding universe. Nevertheless many interesting alternatives to “23/3” were explored. Perhaps the most famous ones are HighLife "23/36" and Diamoeba "5678/35678".
MCell contains many built-in different Life rules. You can read about them in “Life" family.
Cellular automata can be seen as a generalization of Life. Cellular automata are not restricted to 2-dimensional 8-neighbours S/B rules - in different realizations the following items can be changed:
MCell allows exploring Cellular Automata rules with all above extensions (see CA families in MCell).
Although the real Era of Cellular Automata is still expected to come, even today they have proven to be very useful. Some of best known applications of Cellular Automata are:
| Webmaster: Mirek Wojtowicz |
MCell mirrors: |
Last update: 07 Jan 2002